Composite Index Construction
Brief Explanation
An explanation of what indicators are and of the reason why they are widely used in companies and international organizations will be provided. The latest developments in methodology for the construction of indexes and indicators will be explained (economic activity, human development, poverty, finance, etc.). Special attention will be paid to their application in decision-making processes and, more precisely, to their usefulness in the context of forecasting. In particular, the methodology applied by international institutions in the construction of the most commonly known indexes will be explained, identifying and providing potential improvements. Students will solve a case study based on the real situation of an international institution using indicators.
Introduction
A composite indicator measures multi-dimensional concepts (e.g. competitiveness, e-trade or environmental quality) which cannot be captured by a single indicator. Ideally, a composite indicator should be based on a theoretical framework / definition, which allows individual indicators / variables to be selected, combined and weighted in a manner which reflects the dimensions or structure of the phenomena being measure.
Some Examples
Some Composite Indicators:
- Global AgeWatch Index. GAWI.pdf
- HDI. Link Wiki Australia VIDEO
- IQ
- Economic Risk Indicator. Paper.pdf
Another useful applications:
- Forecasting. Forecast.png
- Stress Testing. Density Forecast.
##Data DataSet.pdf
Missing Value Imputation
options(warn = -1)
#Import Data
path <- "compositeIndex"
Data <- read.csv2(paste(path, "Income.csv", sep = "/"))
Data2 <- read.csv2(paste(path, "Index.csv", sep = "/"))
Data <- apply(Data, 2, as.numeric)
Data2 <- apply(Data2, 2, as.numeric)
Data_estimate<-data.frame(Data)
x1<-Data_estimate[,1]
x2<-Data_estimate[,2]
x3<-Data_estimate[,3]
x4<-Data_estimate[,4]
#
dif<-matrix(0,length(x3),1)
dif2<-matrix(0,length(x3),1)
Data_estimate<-data.frame(Data_estimate)
leaps<-regsubsets(x3~x1+x2+x4,data=Data_estimate,nbest=5)
plot(leaps,scale="r2")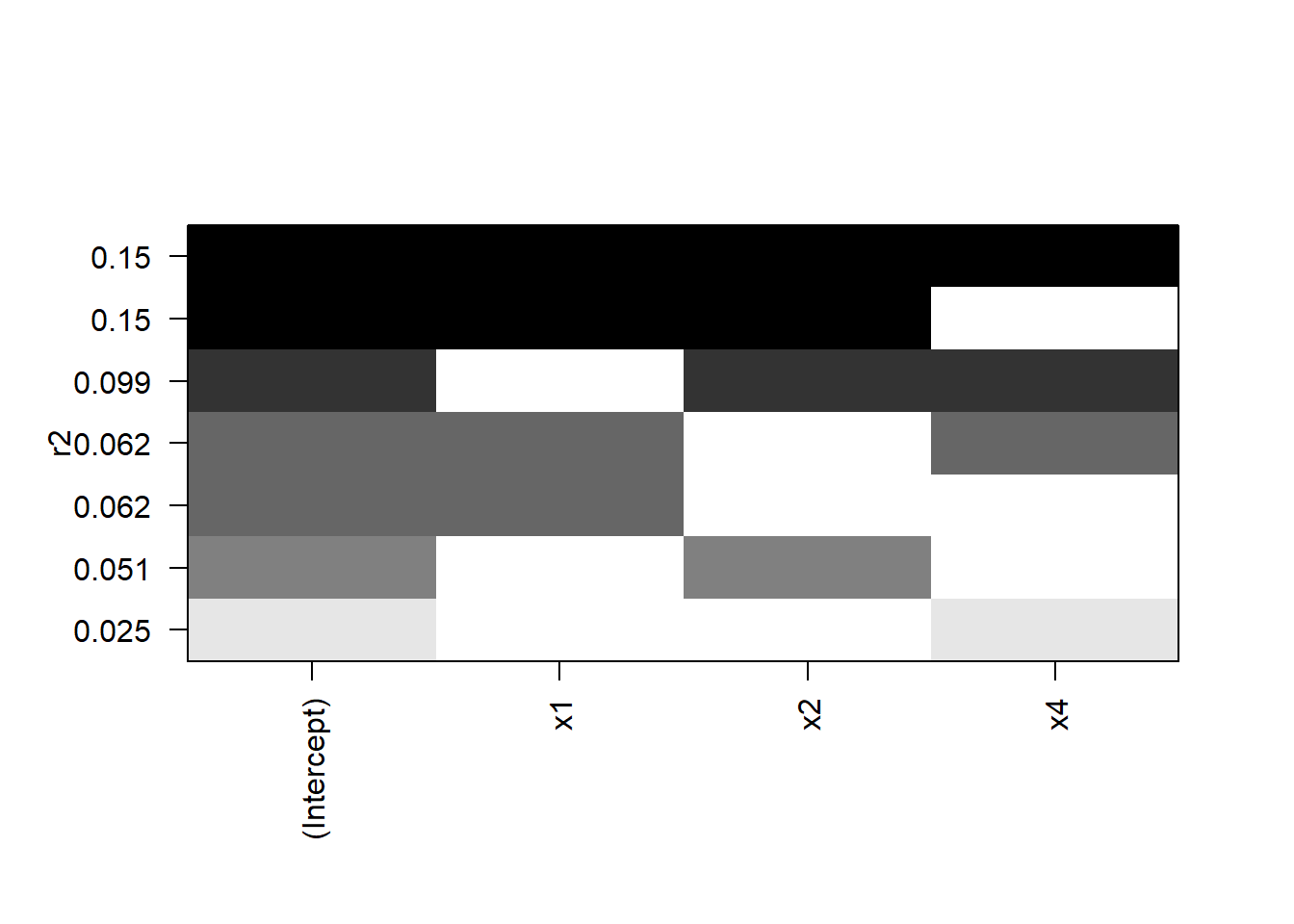
fit <- lm(x3~x1+x2+x4)
for (i in 1:length(x3)) {
value_estimate=fit$coefficients[1]+fit$coefficients[2]*x2[i]+fit$coefficients[3]*x3[i]+fit$coefficients[4]*x4[i]
dif[i]<-abs(x3[i]-value_estimate)/x3[i]
}
for (i in 1:length(x3)) {
Data_estim<-Data
Data_estim[i,3]<-NA
Data_estimate<-data.frame(Data_estim)
a.out <- amelia(Data_estimate, m = 1, boot.type = "none")
unlist(a.out$imputations[[1]])
em_estimation<-as.matrix(a.out$imputations[[1]])
dif2[i]<-abs(x3[i]-em_estimation[i,3])/x3[i]
}
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
##
## -- Imputation 1 --
##
## 1 2 3
Errors=cbind(dif,dif2)
ddf<-data.frame(Errors,GRP = c("Regression","EM"))
boxplot(Errors ~ GRP, main="Relative Welfare",data = ddf, lwd = 1, ylab = 'Errors')
stripchart(Errors~ GRP,vertical = TRUE, data = ddf,
method = "jitter", add = TRUE, pch = 20, col = c('blue','red'),cex=2)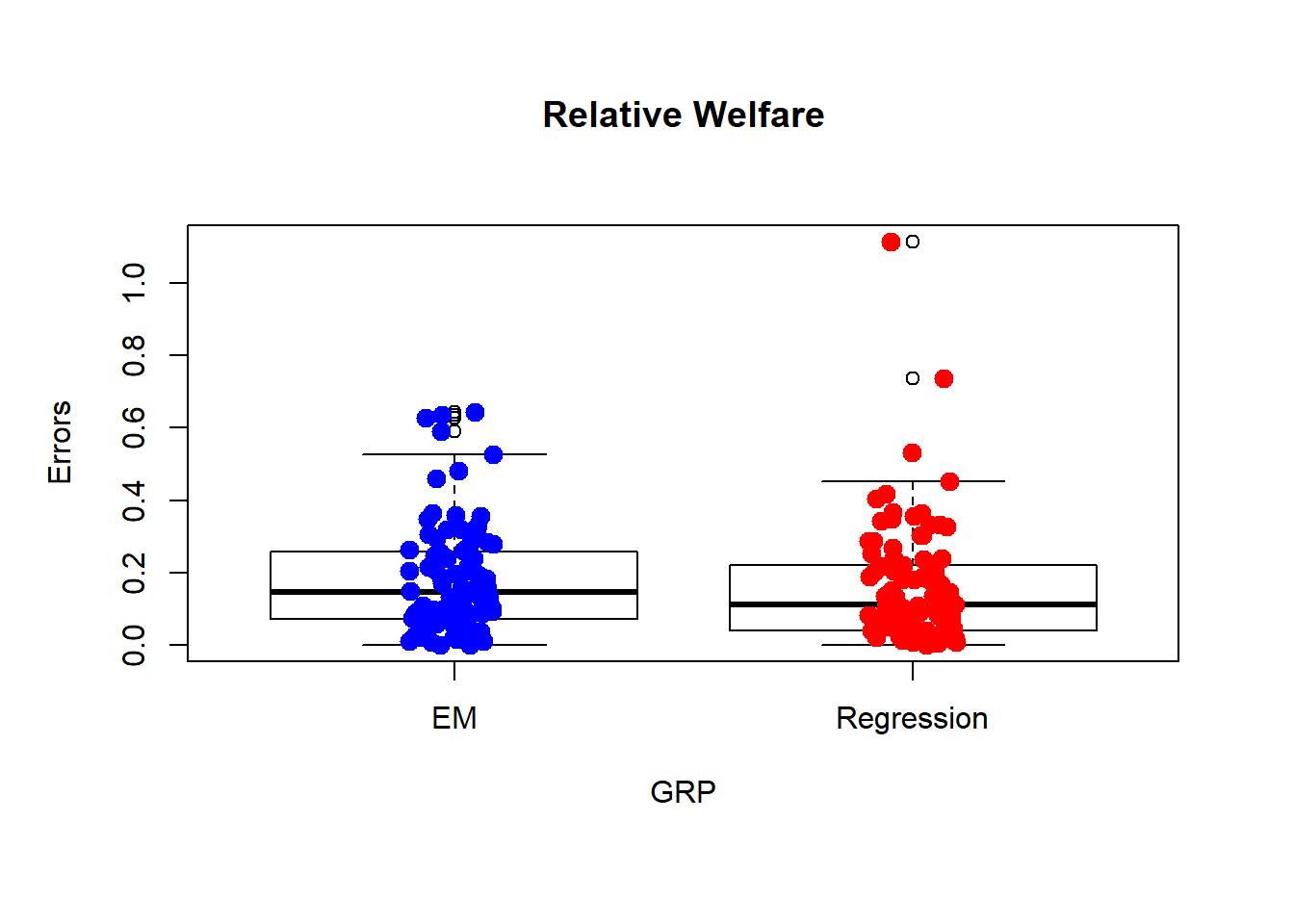
check_value<-mean(dif[!is.na(dif)])
check_value2<-median(dif[!is.na(dif)])
check_value3<-sd(dif[!is.na(dif)])
CV<-c(check_value,check_value2,check_value3)
check_valueb<-mean(dif2[!is.na(dif2)])
check_valueb2<-median(dif2[!is.na(dif2)])
check_valueb3<-sd(dif2[!is.na(dif2)])
CVb<-matrix(c(check_valueb,check_valueb2,check_valueb3),1,3)
C<-matrix(cbind(CV,CVb),2,3)
barplot(C, main="Blue:Regression; Red: EM",
xlab="Mean, Median, StDesv", col=c("darkblue","red"),
beside=TRUE)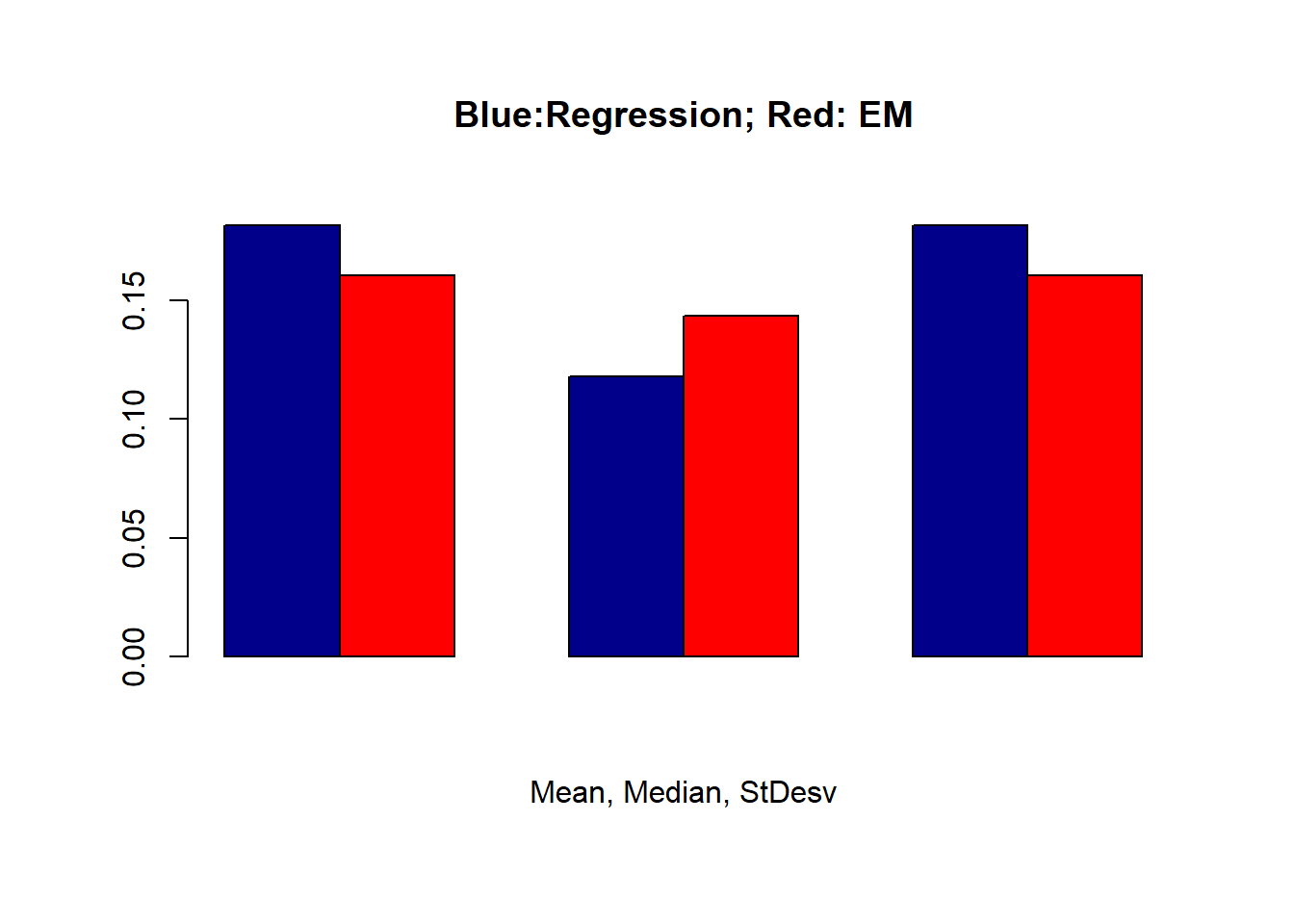
Outlier Detection
Data_estimate<-data.frame(Data)
x1<-Data_estimate[,1]
x2<-Data_estimate[,2]
x3<-Data_estimate[,3]
x4<-Data_estimate[,4]
#Univariate
outlier_values <- boxplot.stats(x3)$out # outlier values.
print(outlier_values)
## [1] 0.5
boxplot(x2, boxwex=1)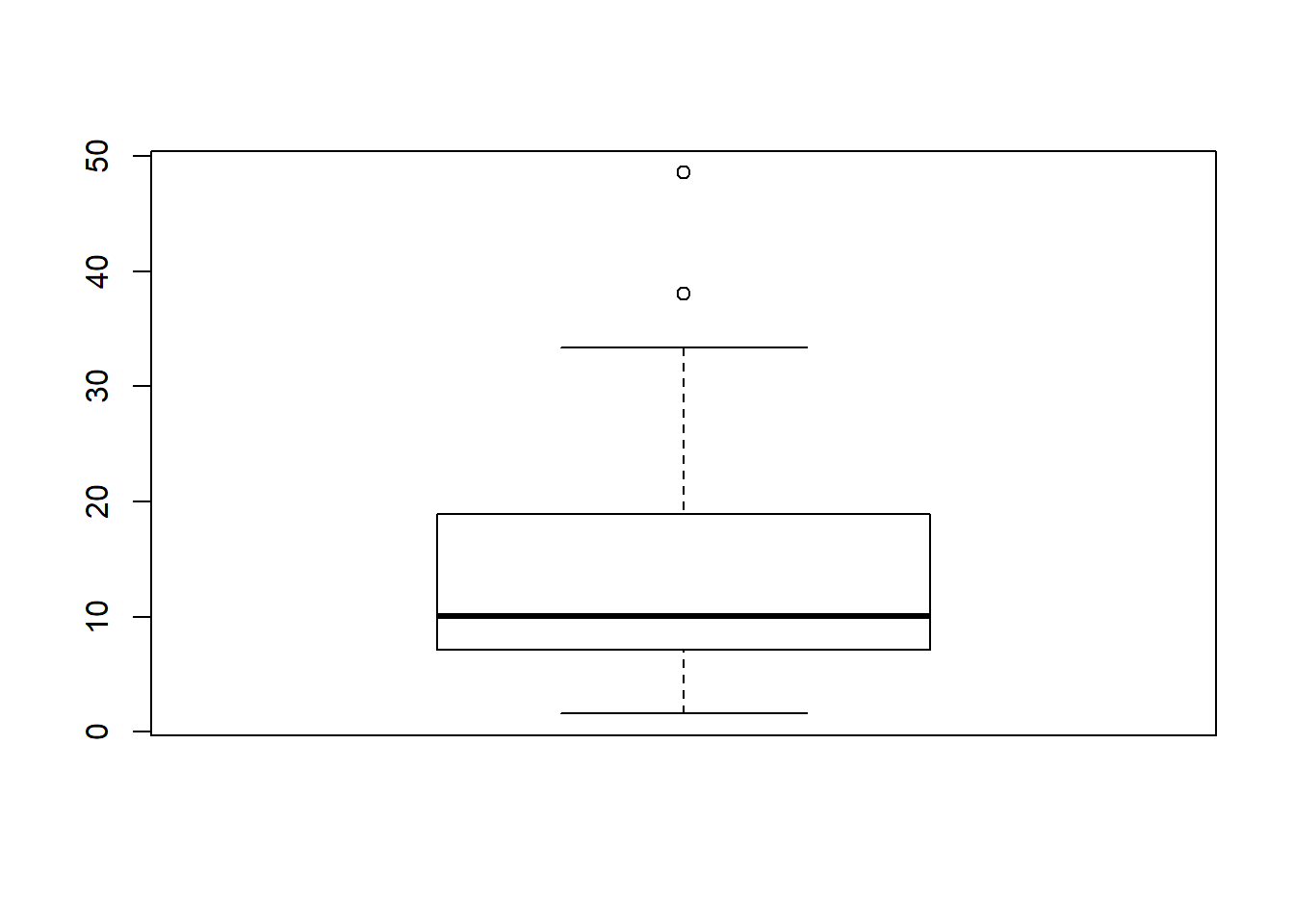
#Multivariate
#Cook DIstance
mod <- lm(x2 ~ ., data=Data_estimate)
cooksd <- cooks.distance(mod)
plot(cooksd, pch="*", cex=2, main="Influential Obs by Cooks distance") # plot cook's distance
abline(h = 4*mean(cooksd, na.rm=T), col="red") # add cutoff line
text(x=1:length(cooksd)+1, y=cooksd, labels=ifelse(cooksd>4*mean(cooksd, na.rm=T),names(cooksd),""), col="red")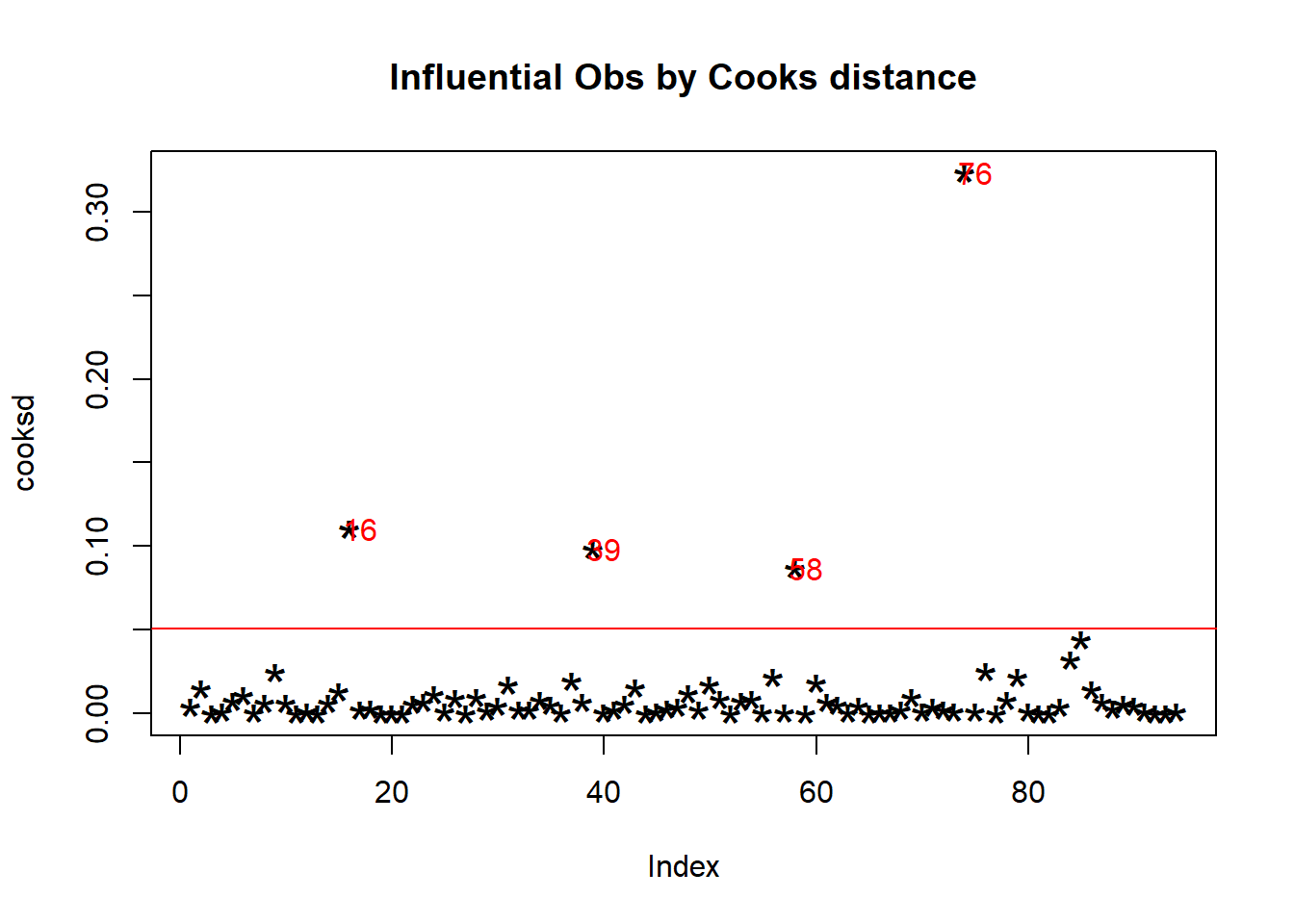
#Mahalanobis Distance
Data2<-Data_estimate[,c(1:3)]
n.outliers <- 2 # Mark as outliers the 2 most extreme points
m.dist.order <- order(mahalanobis(Data2, colMeans(Data2), cov(Data2)), decreasing=TRUE)
is.outlier <- rep(FALSE, nrow(Data2))
is.outlier[m.dist.order[1:n.outliers]] <- TRUE
pch <- is.outlier * 16
col<- is.outlier + 1
plot3d(Data2[,1], Data2[,2], Data2[,3], type="s", col=col,xlab = "Pension",ylab="Poverty",zlab="Welfare")
Normalization
Data2<-Data
for (i in 1:4) {
Data2[,i]<-scale(Data2[,i],TRUE,TRUE)
}
Data3<-Data
for (i in 1:4) {
Data3[,i]<-(Data3[,i]-min(Data3[,i]))/(max(Data3[,i])-min(Data3[,i]))
}
Data4<-Data
for (i in 1:4) {
Data4[,i]<-SoftMax( Data4[,i], lambda = 2, avg = mean( Data4[,i], na.rm = T), std = sd( Data4[,i], na.rm = T))
}
RR<-cor(Data)
RR2<-cor(Data2)
RR3<-cor(Data3)
RR4<-cor(Data4)
dif2<-RR-RR2
dif3<-RR-RR3
dif4<-RR-RR4
check_value<-mean(dif2[!is.na(dif2)])
check_value2<-mean(dif3[!is.na(dif3)])
check_value3<-mean(dif4[!is.na(dif4)])
C<-matrix(c(check_value,check_value2,check_value3),1,3)
barplot(C, main="Changes in Correlation Matrix Structure",
xlab="Z-Score,Max-Min,Softmax",col="blue")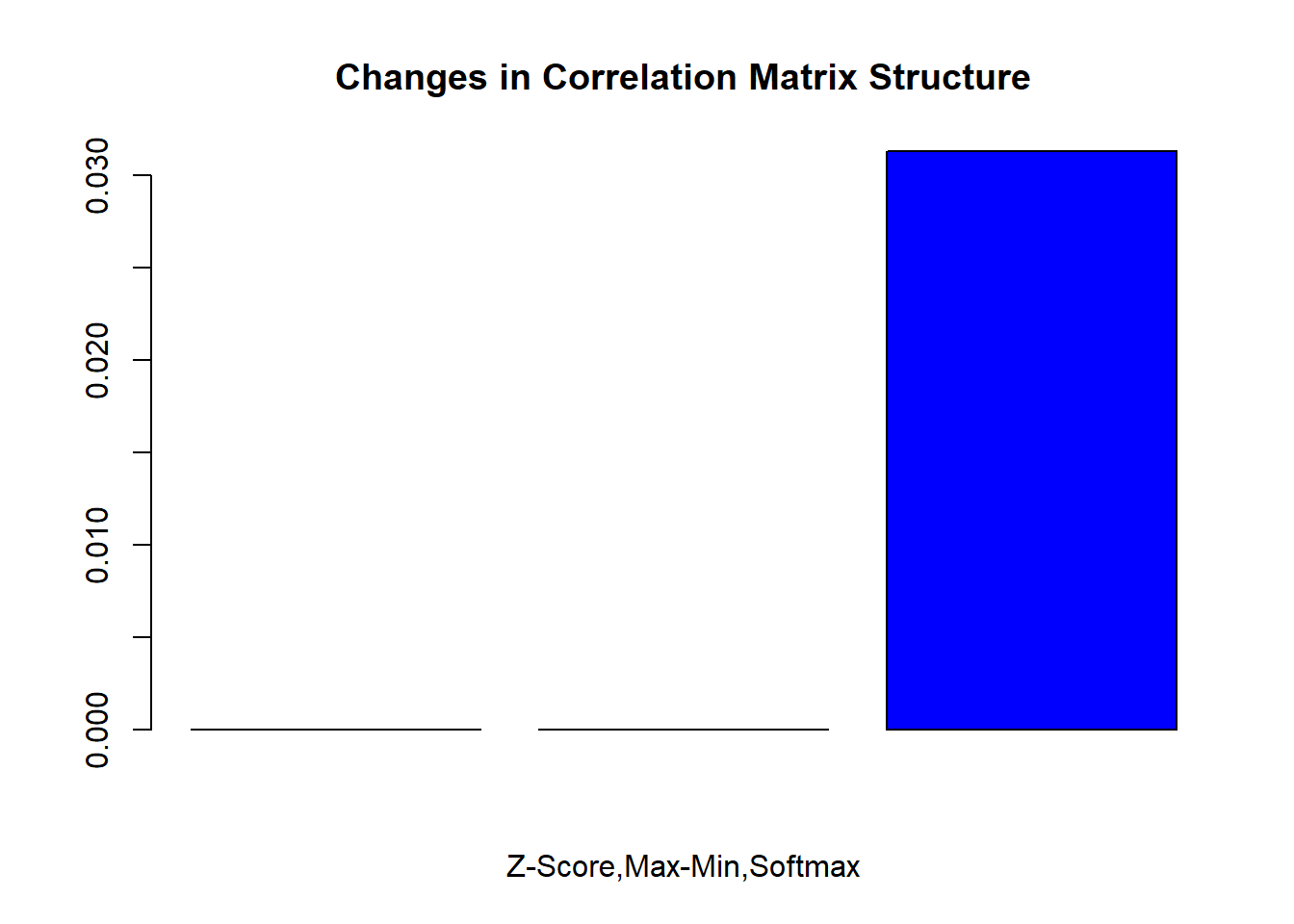
par(mfrow=c(2,2))
hist(Data[,2], col=rgb(0.1,0,1,0.5),xlab="Original",main="Poverty Rate")
hist(Data2[,2], col=rgb(0.1,0,1,0.5),xlab="Standardization",main="Poverty Rate")
hist(Data3[,2], col=rgb(0.1,0,1,0.5),xlab="Max.Min",main="Poverty Rate")
hist(Data3[,2], col=rgb(0.1,0,1,0.5),xlab="SoftMax",main="Poverty Rate")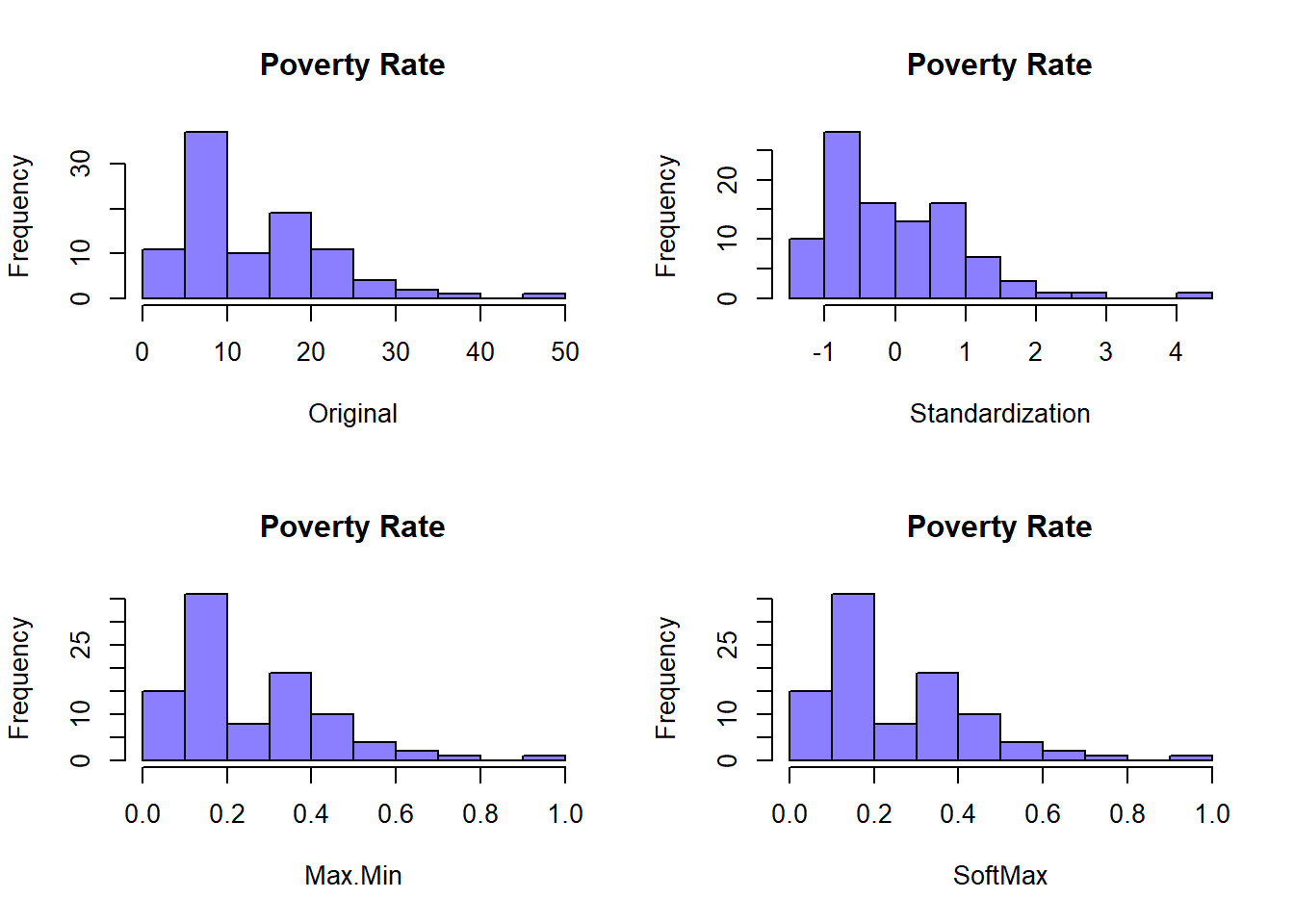
Original<-matrix(0,99,1)
Zscore<-matrix(0,99,1)
Max.Min<-matrix(0,99,1)
softmax<-matrix(0,99,1)
z<-matrix(seq(0.01,0.99,0.01),99,1)
for ( i in c(1:99)) {
Original[i]<-quantile(Data[,2],z[i])
Zscore[i]<-quantile(Data2[,2],z[i])
Max.Min[i]<-quantile(Data3[,2],z[i])
softmax[i]<-quantile(Data4[,2],z[i])
}
dat<-data.frame(Original,Zscore)
dat2<-data.frame(Original,Max.Min)
dat3<-data.frame(Original,softmax)
ggplot(dat, aes(x=Original, y=Zscore)) +
geom_point(shape=1) + # Use hollow circles
geom_smooth(method=lm,level=0.9) 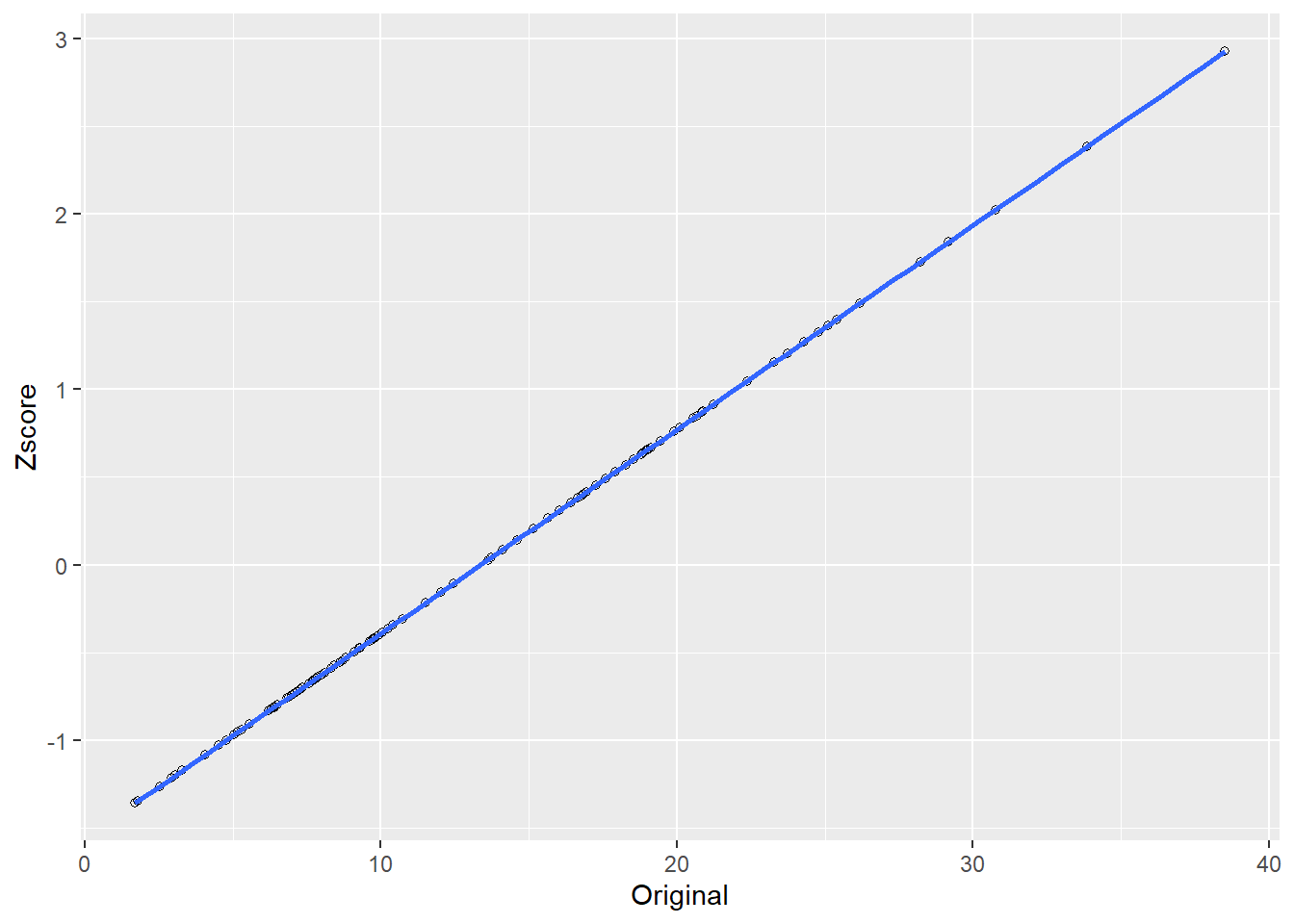
ggplot(dat2, aes(x=Original, y=Max.Min)) +
geom_point(shape=1) + # Use hollow circles
geom_smooth(method=lm,level=0.9) 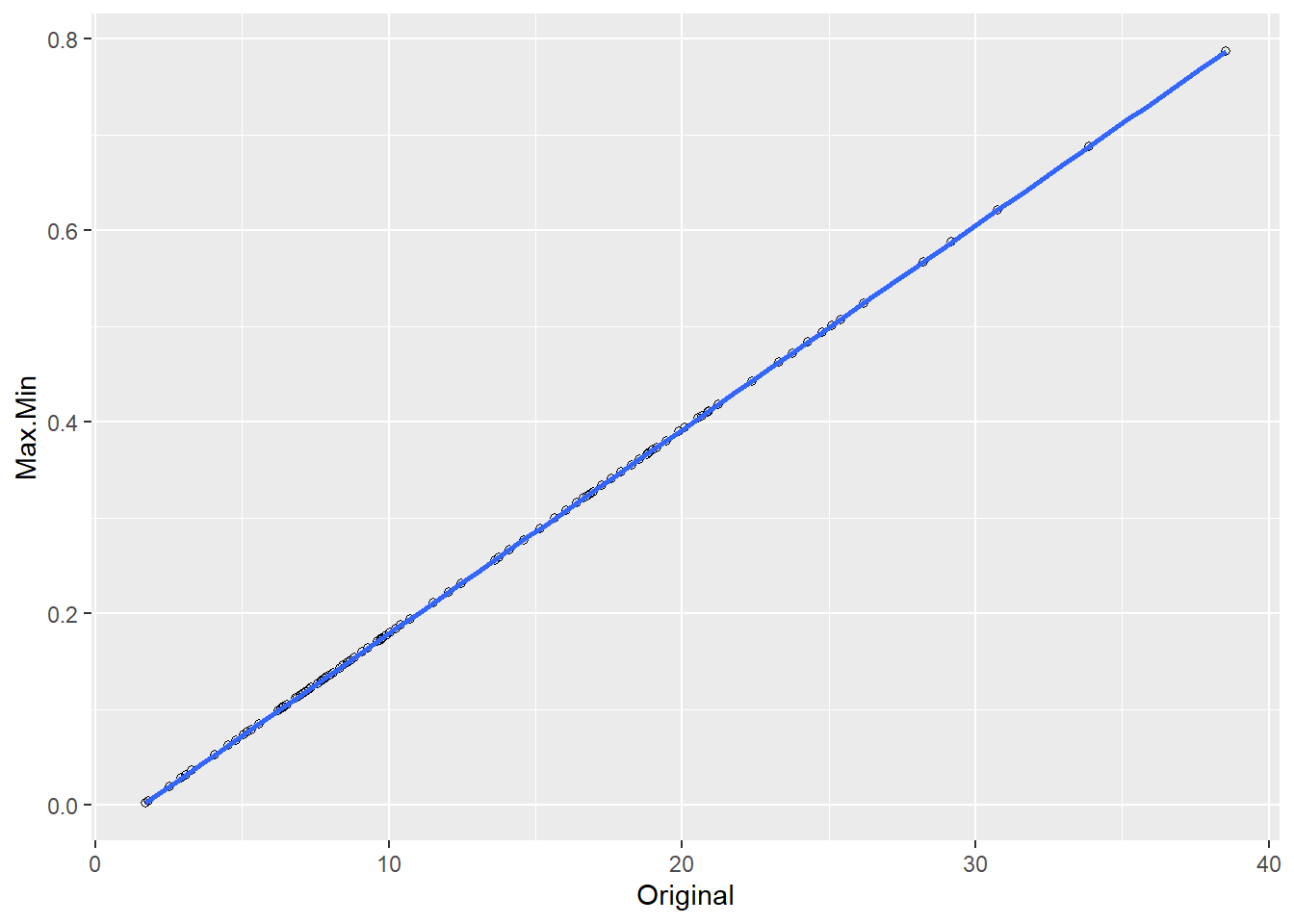
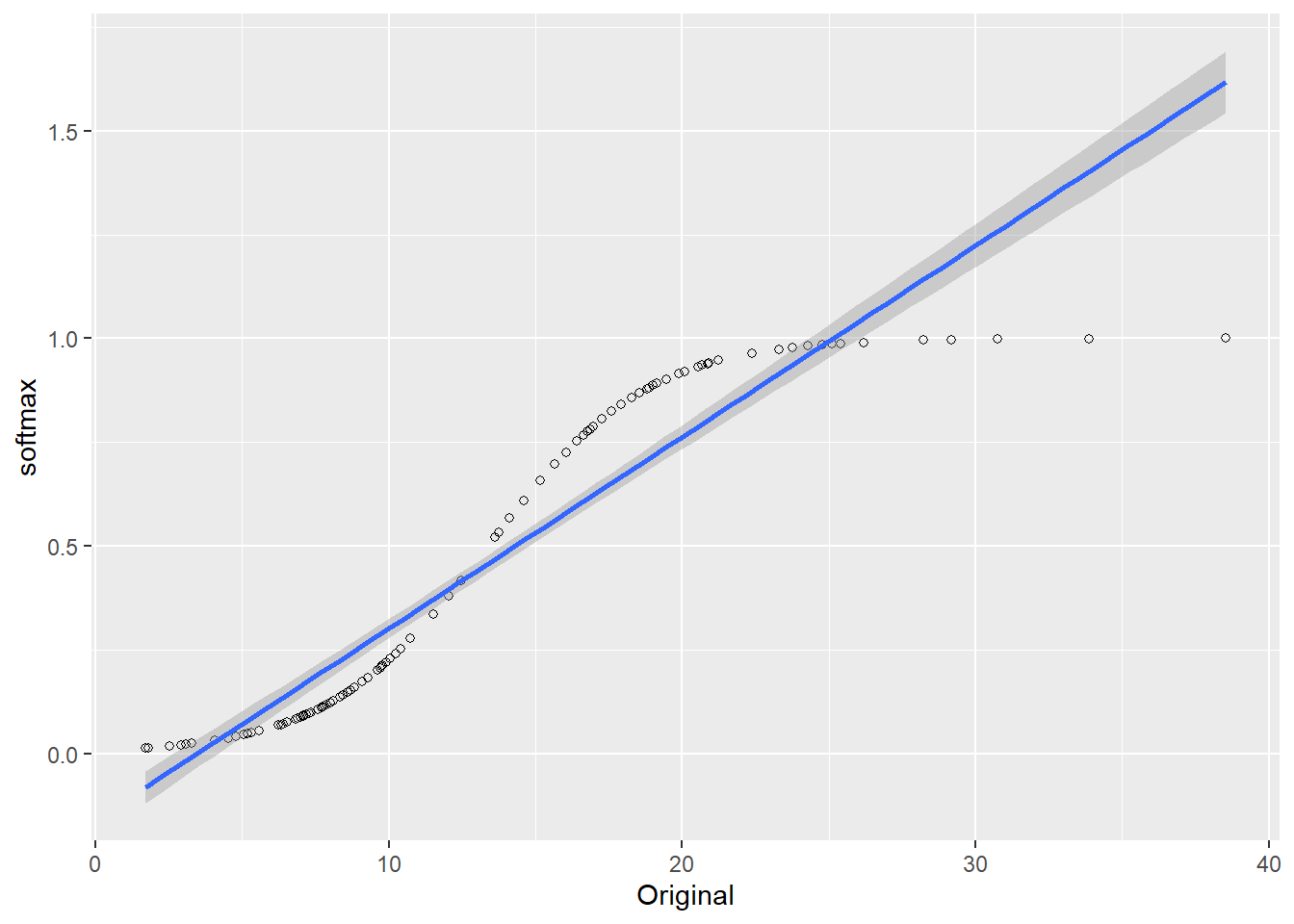
ggplot(dat3, aes(x=Original, y=softmax)) +
geom_point(shape=1) + # Use hollow circles
geom_smooth(method=lm,level=0.9)