# We can call to the needed libraries or load the data sets we are going to use.
# echo, message, warning =FALSE because we do not want messages, warnings and Rcode in the final output
library(knitr) #for nice tables
library(stats); library(graphics) #needed for the data set and some statistics

In the first session we learnt how to produce formatted output automatically from a .Rmd file that combines text and some R code. For doing so, we introduced R notebook and Rmarkdown. R notebook is an R Markdown document with chunks that can be executed independently and interactively, with output visible immediately beneath the input. Finally, we understood the workflow (Knitr+PANDOC) that produces the final output.

This is an example of Rmarkdown document that you could use as starting point or as a template for future projects, we tried to use mostly all the commands we explained during the session. You can download the file here and the Cheat Sheet. For further reading, this is an amaizing source Rmarkdown: The Definitive Guide.

All the content contained is based on Wikipedia and the code was taken from the R help of the data set “anscombe”.

#Introduction Anscombe’s quartet comprises four datasets that have nearly identical simple descriptive statistics, yet appear very different when graphed. Each dataset consists of eleven points in \(\mathbb{R}^2\). They were constructed in 1973 by the statistician Francis J. Anscombe to demonstrate both the importance of graphing data before analyzing it and the effect of outliers on statistical properties. He described the article as being intended to attack the impression among statisticians that “numerical calculations are exact, but graphs are rough”. For more details you can find his article Graphs in statistical analysis (1973) published in the journal American Statistician.

The data set

Here we load the data set and print the variables using the kable function from knitr package. One could observe how the values of all the variables look roughly equal. However, the small disparities make a big difference.

data("anscombe")
kable(anscombe, caption = "Here we have our data set")
Here we have our data set
x1 x2 x3 x4 y1 y2 y3 y4
10 10 10 8 8.0 9.1 7.5 6.6
8 8 8 8 7.0 8.1 6.8 5.8
13 13 13 8 7.6 8.7 12.7 7.7
9 9 9 8 8.8 8.8 7.1 8.8
11 11 11 8 8.3 9.3 7.8 8.5
14 14 14 8 10.0 8.1 8.8 7.0
6 6 6 8 7.2 6.1 6.1 5.2
4 4 4 19 4.3 3.1 5.4 12.5
12 12 12 8 10.8 9.1 8.2 5.6
7 7 7 8 4.8 7.3 6.4 7.9
5 5 5 8 5.7 4.7 5.7 6.9

#Numerical Analysis ## Some descriptive statistics Let compute some statistics. We are going to see how the results for each variable are more or less similar.

stat<-summary(anscombe)

kable(stat[,5:8], caption = "Descriptive statistics")
Descriptive statistics
y1 y2 y3 y4
Min. : 4.3 Min. :3.1 Min. : 5.4 Min. : 5.2
1st Qu.: 6.3 1st Qu.:6.7 1st Qu.: 6.2 1st Qu.: 6.2
Median : 7.6 Median :8.1 Median : 7.1 Median : 7.0
Mean : 7.5 Mean :7.5 Mean : 7.5 Mean : 7.5
3rd Qu.: 8.6 3rd Qu.:8.9 3rd Qu.: 8.0 3rd Qu.: 8.2
Max. :10.8 Max. :9.3 Max. :12.7 Max. :12.5 
kable(round(t(sapply(anscombe, var)[5:8]),digits = 2), caption = "Variances")
Variances
y1 y2 y3 y4
4.1 4.1 4.1 4.1

Linear Regression

Here we go with some formulas, if you need help with some command just look for LATEX math mode in internet or check this web.

Given two variables \(Y\) and \(X\), we assume that the variables follow a linear relationship such that \[Y = \beta_0+\beta_1*X+\epsilon,\] being \(\epsilon\) a independent and identically distributed random variable from a normal distribution \(\epsilon \sim N(0,1)\). We can estimate the parameters by minimizing the mean square error, i.e. \[\min_{ \{\beta_0,\beta_1\}} \sum_{i=1}^n (y_i-\beta_0-\beta_1*x_i)^2,\] ending up with \[\hat{\beta_1}=\frac{Cov(X,Y)}{V(X)},\] \[\hat{\beta_0}= \bar{Y}-\bar{X}*\beta_1.\]

In the following code chunk, the linear regression model are adjusted to the 4 variables. The parameters, standar errors, t-values and p-values are roughly the same.

## now some "magic" to do the 4 regressions in a loop:
ff <- y ~ x
mods <- setNames(as.list(1:4), paste0("lm", 1:4))
for(i in 1:4) {
  ff[2:3] <- lapply(paste0(c("y","x"), i), as.name)
  mods[[i]] <- lmi <- lm(ff, data = anscombe)
}

kable(lapply(mods[1:2], function(fm) coef(summary(fm))), caption='Regressions')
Regressions
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0 1.12 2.7 0.03
x1 0.5 0.12 4.2 0.00
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0 1.13 2.7 0.03
x2 0.5 0.12 4.2 0.00 
kable(lapply(mods[3:4], function(fm) coef(summary(fm))), caption='Regressions')
Regressions
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0 1.12 2.7 0.03
x3 0.5 0.12 4.2 0.00
Estimate Std. Error t value Pr(>|t|)
(Intercept) 3.0 1.12 2.7 0.03
x4 0.5 0.12 4.2 0.00

#Graphical analysis

A simple plot can bring to light that the 4 variables are very different one from another.

op <- par(mfrow = c(2, 2), mar = 0.1+c(4,4,1,1), oma =  c(0, 0, 2, 0))
for(i in 1:4) {
  ff[2:3] <- lapply(paste0(c("y","x"), i), as.name)
  plot(ff, data = anscombe, col = "red", pch = 21, bg = "orange", cex = 1.2,
       xlim = c(3, 19), ylim = c(3, 13))
    abline(mods[[i]], col = "blue")
}
mtext("Anscombe's data sets", outer = TRUE, cex = 1.5)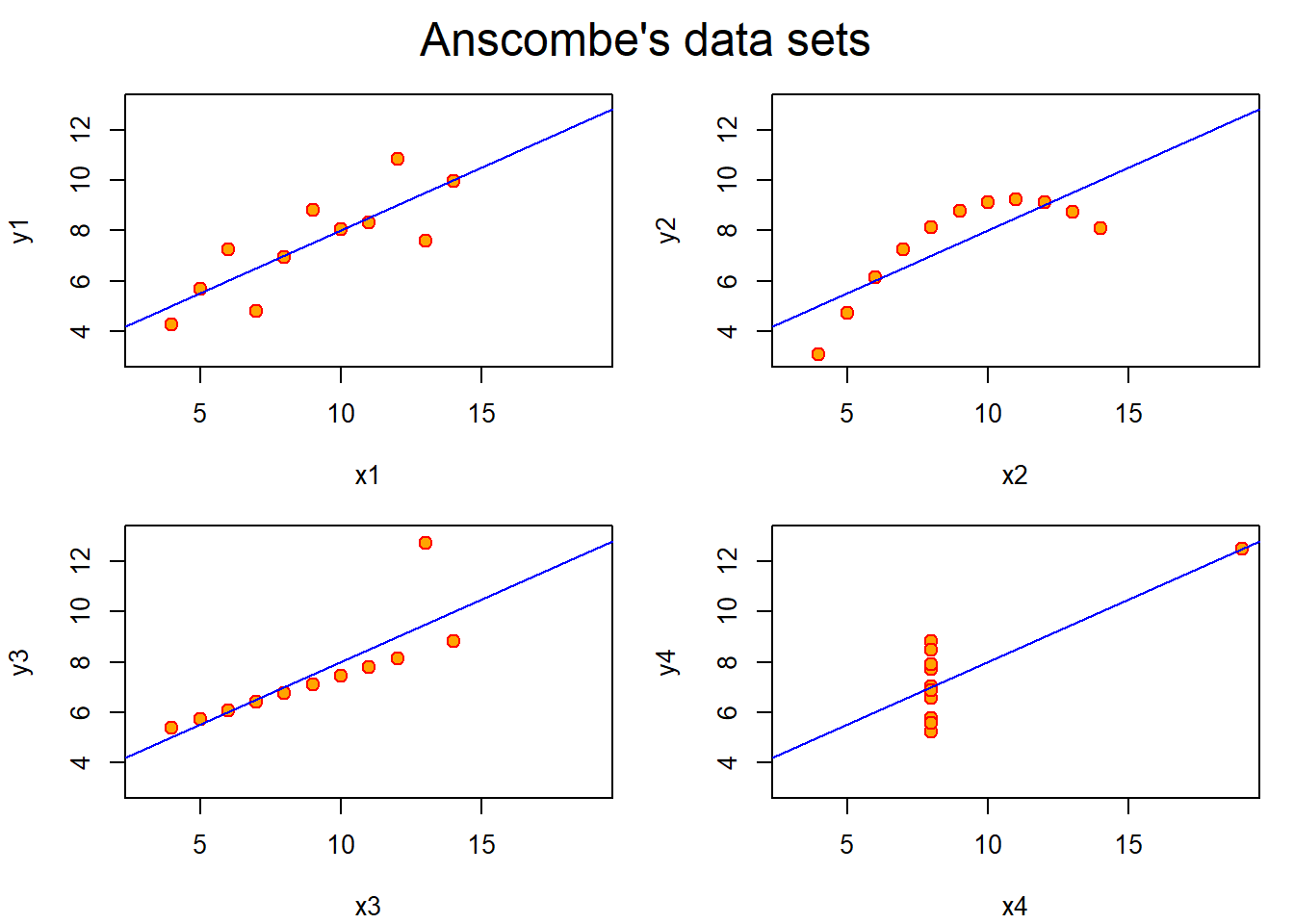

  1. The first scatter plot (top left) appears to be a simple linear relationship, corresponding to two variables correlated and following the assumption of normality of the linear regression model.
  2. The second graph (top right) is not distributed normally; while a relationship between the two variables is obvious, it is not linear, and the Pearson correlation coefficient is not relevant because it was defined for measuring linear relationship.
  3. In the third graph (bottom left), the distribution is linear, but should have a different regression line (a robust regression would have been called for). The calculated regression is offset by the one outlier which exerts enough influence to lower the correlation coefficient from 1 to 0.816.
  4. Finally, the fourth graph (bottom right) shows an example when one outlier is enough to produce a high correlation coefficient, even though the other data points do not indicate any relationship between the variables.

Conclusion

“Numerical calculations are exact, but graphs are rough”.