Statistical properties of partially observed integrated functional depths

Authors

Affiliations

Antonio Elías

Universidad de Málaga, Málaga, Spain

Stanislav Nagy

Charles University, Prague, Czech Republic

Important links

• Article Open Access
• GitHub repository
• R-package CRAN

Abstract

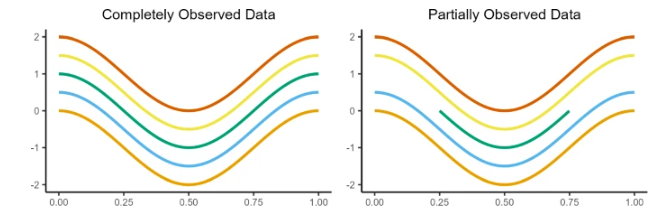
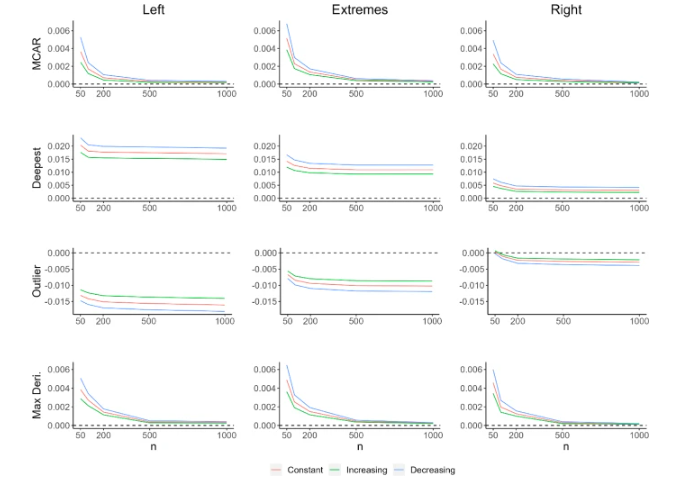
Integrated functional depths (IFDs) present a versatile toolbox of methods introducing notions of ordering, quantiles, and rankings into a functional data analysis context. They provide fundamental tools for nonparametric inference of infinite-dimensional data. Recently, the literature has extended IFDs to address the challenges posed by partial observability of functional data, commonly encountered in practice. That resulted in the development of partially observed integrated functional depths (POIFDs). POIFDs have demonstrated good empirical results in simulated experiments and real problems. However, there are still no theoretical results in line with the state of the art of IFDs. This article addresses this gap by providing theoretical support for POIFDs, including (i) uniform consistency of their sample versions, (ii) weak continuity with respect to the underlying probability measure, and (iii) uniform consistency for discretely observed functional data. Finally, we present a sensitivity analysis that evaluates how our theoretical results are affected by violations of the main assumptions.

Figure 1: Functional Data Analysis and a simple scenenario of Partially Observed Data Analysis. Only with a standardized weight the green curve is the deepest in the partially observed data setup.

Figure 4: Estimation bias when sample size growths under violations of the MCAR assumption. Not all the types of violations bias the estimation of the depths.

Citation

@Article{Elias2024,
author={El{\'i}as, Antonio
and Nagy, Stanislav},
title={Statistical properties of partially observed integrated functional depths},
journal={TEST},
year={2024},
month={Nov},
day={20},
abstract={Integrated functional depths (IFDs) present a versatile toolbox of methods introducing notions of ordering, quantiles, and rankings into a functional data analysis context. They provide fundamental tools for nonparametric inference of infinite-dimensional data.  Recently, the literature has extended IFDs to address the challenges posed by partial observability of functional data, commonly encountered in practice. That resulted in the development of partially observed integrated functional depths (POIFDs). POIFDs have demonstrated good empirical results in simulated experiments and real problems. However, there are still no theoretical results in line with the state of the art of IFDs. This article addresses this gap by providing theoretical support for POIFDs, including (i) uniform consistency of their sample versions, (ii) weak continuity with respect to the underlying probability measure, and (iii) uniform consistency for discretely observed functional data. Finally, we present a sensitivity analysis that evaluates how our theoretical results are affected by violations of the main assumptions.},
issn={1863-8260},
doi={10.1007/s11749-024-00954-6},
url={https://doi.org/10.1007/s11749-024-00954-6}
}