Localization processes for functional data analysis

Authors

Affiliations

Antonio Elías

Universidad de Málaga, Málaga, Spain

Raúl Jiménez

Universidad Carlos III de Madrid, Madrid, Spain

Joe Yukich

Lehigh University, Pensilvania, United States

Important links

• ArXiv Preprint
• R-package CRAN
• GitHub repository

Abstract

We propose an alternative to k-nearest neighbors for functional data whereby the approximating neighboring curves are piecewise functions built from a functional sample. Using a locally defined distance function that satisfies stabilization criteria, we establish pointwise and global approximation results in function spaces when the number of data curves is large. We exploit this feature to develop the asymptotic theory when a finite number of curves is observed at time-points given by an i.i.d. sample whose cardinality increases up to infinity. We use these results to investigate the problem of estimating unobserved segments of a partially observed functional data sample as well as to study the problem of functional classification and outlier detection. For such problems our methods are competitive with and sometimes superior to benchmark predictions in the field. The R package localFDA provides routines for computing the localization processes and the estimators proposed in this article.

Important figures

Figure 5: Probailities estimation

Figure 5: Outputs from the outlier detection methods under consideration. All the methods detect Okinawa. Outliergram and localization distance boxplots agree with respect to Fukui and Kochi. The localization distances are the only ones able to detect Aomori as an extreme outlier and the only ones indicating a certain atypicity of Tokyo. For a few values of k, the localization distances corresponding to Nagano, Shiga and Kanagawa fell above (but close to) the default whiskers.

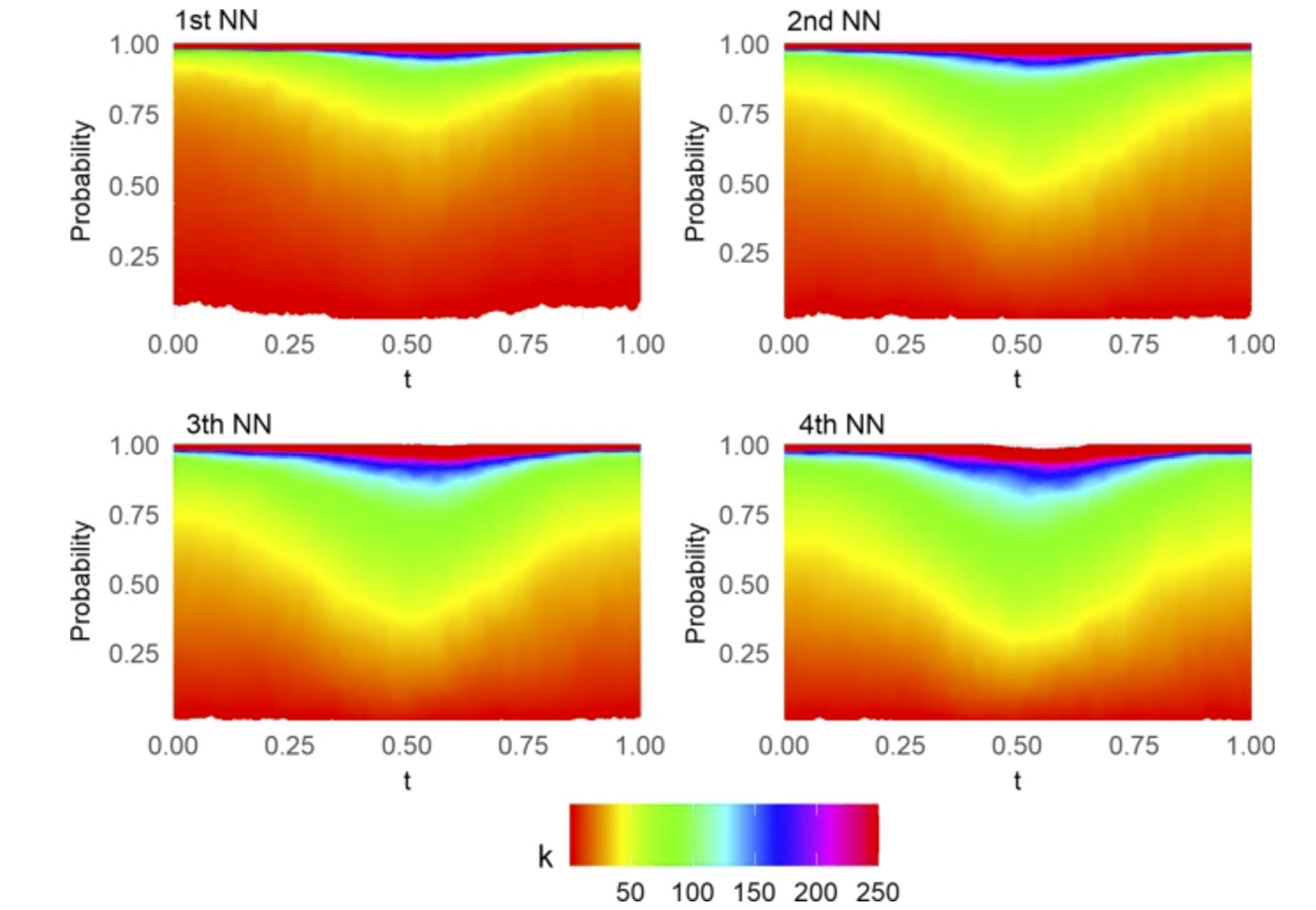
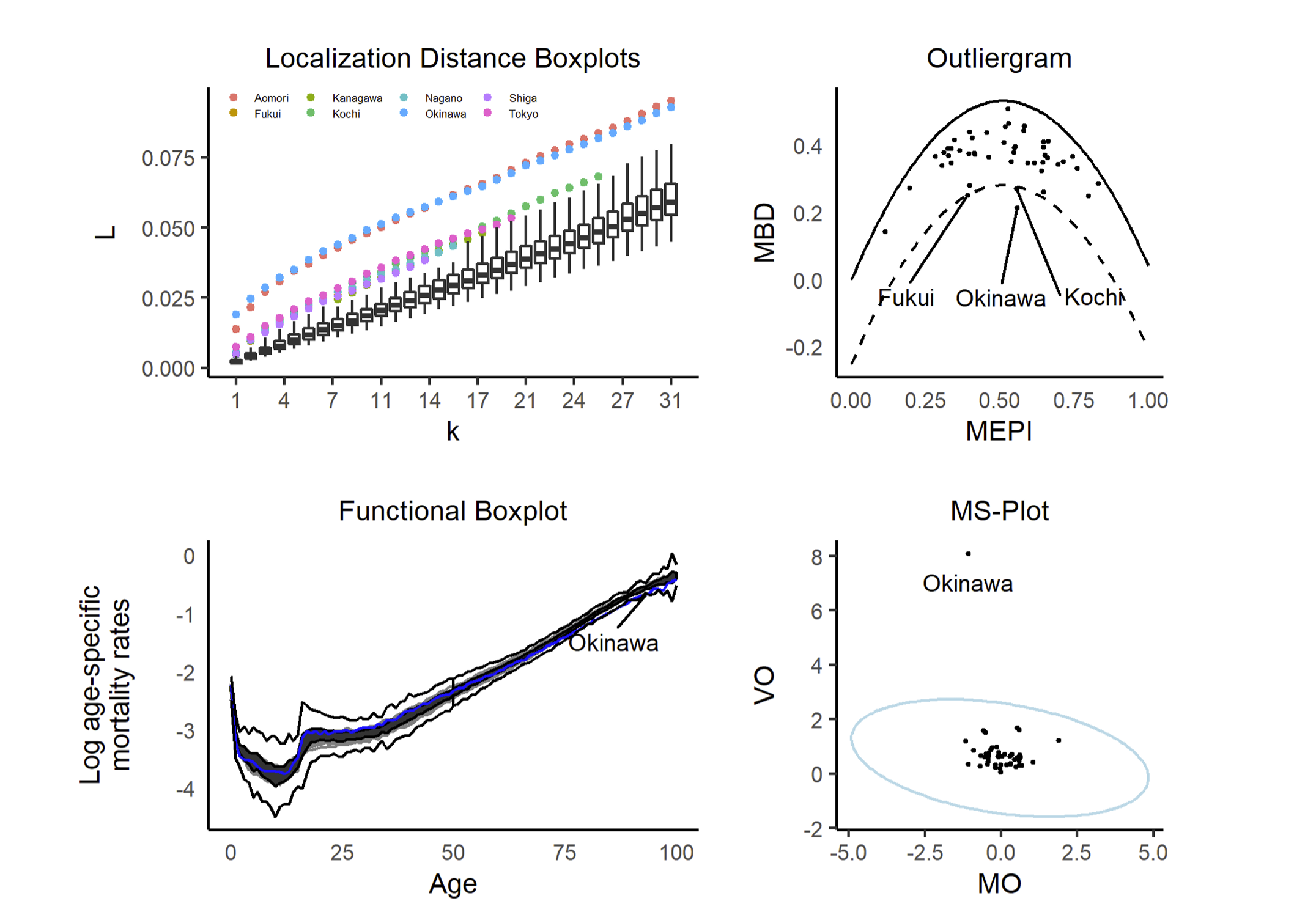
Citation

@Article{ElíasADAC2023,
author={El{\'i}as, Antonio
and Jim{\'e}nez, Ra{\'u}l
and Yukich, J. E.},
title={Localization processes for functional data analysis},
journal={Advances in Data Analysis and Classification},
year={2023},
month={Jun},
day={01},
volume={17},
number={2},
pages={485-517},
abstract={We propose an alternative to k-nearest neighbors for functional data whereby the approximating neighboring curves are piecewise functions built from a functional sample. Using a locally defined distance function that satisfies stabilization criteria, we establish pointwise and global approximation results in function spaces when the number of data curves is large. We exploit this feature to develop the asymptotic theory when a finite number of curves is observed at time-points given by an i.i.d. sample whose cardinality increases up to infinity. We use these results to investigate the problem of estimating unobserved segments of a partially observed functional data sample as well as to study the problem of functional classification and outlier detection. For such problems our methods are competitive with and sometimes superior to benchmark predictions in the field. The R package localFDA provides routines for computing the localization processes and the estimators proposed in this article.},
issn={1862-5355},
doi={10.1007/s11634-022-00512-8},
url={https://doi.org/10.1007/s11634-022-00512-8}
}